Первичные дирекции, часть IV
В этой статье
Если сигнификатор, который
ты хочешь направитьк градусу эклиптики, расположенна Асценденте, вычти косое восхождение градуса, которыйты хочешь направить,из косого восхождения градуса,к которому ты направляешь. Остаток — градусы дирекции.
Если сигнификаторв градусе седьмого, вычти вычти косое восхождение градуса противоположного тому,в котором сигнификатор,из косого восхождения градуса противоположного тому,к которому ты хочешь направить.
Если сигнификаторв Середине Неба илив подземном углу, вычти прямое восхождение градуса сигнификатораиз прямого восхождения градуса,к которому хочешь направить.Остаток — градусы дирекции.
Затем
Если сигнификатор, который
ты хочешь направить, нев одном из этих четырёх углов, возьми расстояниеот одного из двух углов,а именно Середины Неба или подземного угла.То есть посмотри, если сигнификатор между Асцендентоми Серединой Неба, вычти прямое восхождение градуса Середины Небаиз прямого восхождения градуса сигнификатора;а если он между седьмыми Серединой Неба, вычти прямое восхождение градуса сигнификатораиз прямого восхождения градуса Середины Неба. То, что останетсяв этих двух случаях, разделина величину дневного часа градуса,в котором расположен сигнификатор. Результатом будет часовое расстояниеот угла.
Если между Асцендентоми подземным углом, вычти прямое восхождение градуса сигнификатораиз прямого восхождения градуса подземного угла.Если между подземным угломи седьмым, вычти прямое восхождение градуса подземного углаиз прямого восхождения градуса сигнификатора. То, что останетсяв каждом из этих двух случаев, разделина величину дневного часа градуса противоположного градусу сигнификатора.Результат — часовое расстояниеот угла.
То есть, прежде всего,
Когда
ты знаешь часовое расстояниеот угла и желаешь направить сигнификаторк точке эклиптики,а сигнификатор находитсяв восточной полусфере, котораяот Середины Небадо подземного угла, следуя через Асцендент, вычти прямое восхождение градуса сигнификатора, которыйты хочешь направить,из прямого восхождения градуса,к которому ты хочешь направить.Остаток — показатель прямого восхождения. Запомни его. Затем вычти косое восхождение градуса,в котором находится сигнификатор,из косого восхождения градуса,к которому ты хочешь его направить. То, что останется, будет показателем косого восхождения. Затем возьми разницу между показателем прямого восхожденияи показателем косого восхождения. Затем возьмиеё шестую частьи умножь на часовое расстояниеот угла. Результатом будет поправка.Если показатель прямого восхождения меньше показателя косого восхождения, прибавь поправкук показателю прямого восхождения.Если показатель прямого восхождения больше, вычтииз него поправку.Что получится — дуга дирекции.
А если сигнификатор находится
Это сердцевина алгоритма, суть средневекового способа вычисления первичных дирекций. Давайте последуем рассуждениям средневековых астрологов, чтобы понять, что
Они знали, что точки горизонта должны направляться по косому восхождению (или захождению), точки меридиана должны направляться по прямому восхождению.
Как Али ибн Ридван говорит
И поэтому дирекция
в этом случае должна быть сделана по восхождению смешанномуиз восхождения места рожденияи восхождения прямого круга.
Очевидно, что чем ближе точка
Птолемей анализирует свой пример, который
Но по
тому же методу оно проходило46 периодов, когда место пророгации восходило,58 — когда место пророгации былов Середине Неба, и70 — когда оно заходило.
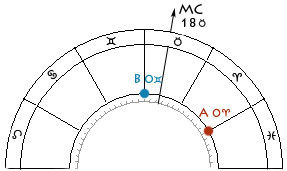
То есть, если сигнификатор (0° Овна)
Таким образом, число экваториальных периодов для точки между Серединой Неба
и Западом отличаетсяот каждого из остальных. Так оно равно 64,а разность пропорциональна разницев три часа, поскольку она составляла12 экваториальных периодов, когда речь шлао других квадрантах между центрами,и только 6 экваториальных периодовв случае расстоянияв три часа.
Сигнификатор отстоит
А половина от
И если
Это
Ввиду того, что приблизительно одинаковое пропорциональное соотношение наблюдается
во всех случаях, возможен более простой путь использования метода. Так, когда предшествующий градус восходит, томы будем использовать восхождения вплотьдо последующего градуса; еслион приходится на Середину Неба,то — восхождения прямой небесной сфере,если же он заходит, то — нисхождения. Однаков случае его расположения между этими точками, например,на вышеописанном расстоянииот Овна, нам следует взять вначале экваториальные периоды, соответствующие каждомуиз окружающих углов,и тогда мы обнаружим, что поскольку начало Овна, по нашему предположению, находитсяза верхней Серединой Неба,и расположено между нейи Западом, экваториальные периодыот Середины Неба иот Запада до начала Близнецов будут соответственно равны58 и 70. Затем установим, как было показано выше,на сколько обычных часов предшествующий отрезок удалёнот каждого из углов и какую долю они могут составитьот шести обычных часов квадранта;мы будем добавлять или вычитать
из угла, с которым производится сравнение, эту долю разности между обеими суммами. Например, поскольку разность между упомянутыми выше величинами70 и 58 равна 12 периодам и предполагалось, что предшествующее место удаленоот каждого углана равное количество обычных часов, то есть 3, что составляет половину от 6, то взяв также половину от12 экваториальных периодови либо прибавив её к 58, либо отняв от 70,мы получим результат, соответствующий64 периодам.
И это
Давайте рассчитаем пример Птолемея по алгоритму

Сигнификатор расположен между Серединой Неба
Прежде всего,
0° Весов:
косое восхождение 180°0′;
прямое восхождение 180°0′.
0° Стрельца:
косое восхождение 250°45′;
прямое восхождение 237°46′.
Теперь
237°46′ – 180°0′ = 57°46′
250°45′ – 180°0′ = 70°45′
Теперь надо найти разницу между этими двумя показателями:
70°45′ – 57°46′ = 12°59′
Теперь нам надо
12°59′:
2°9′50′′ × 2.9989 = 6°29′21′′
Мы прибавляем это
57°46′ + 6°29′21′′ = 64°15′21′′
Когда мы в предыдущей статье рассчитывали дугу дирекции по первому алгоритму Птолемея,
Таким образом,
октябрь 2003
